Några klassiska krypteringstekniker¶
Caesarchiffret har fått sitt namn från Julius Caesar, som enligt historiska källor använde en enkel förskjutning av alfabetet när han skickade militära meddelanden.
Vigenèrechiffret utvecklades på 1500-talet och bygger på idén att använda flera olika förskjutningar styrda av ett nyckelord.
Under lång tid kallades Vigenèrechiffret för ”det oknäckbara chiffret”, eftersom det var betydligt säkrare än enkla substitutionschiffer.
Först på 1800-talet utvecklades metoder för att systematiskt bryta det, vilket visade att även mer avancerade handchiffer kunde ha svagheter.
Båda metoderna är idag lätta att knäcka med datorer, men de illustrerar viktiga idéer i kryptografi — särskilt hur moduloaritmetik används för att låta alfabetet “loopa runt”.
Syftet med övningen¶
Efter övningen ska du kunna:
- Förklara varför moduloräkning är nödvändig när man arbetar med alfabetet i kryptering.
- Koda och avkoda med Caesar-chiffer och förstå den matematiska principen bakom.
- Beskriva hur Vigenère-chiffret fungerar och hur det skiljer sig från Caesar-chiffret.
- Översätta text till talsekvenser och utföra beräkningar på dessa med hjälp av moduloaritmetik.
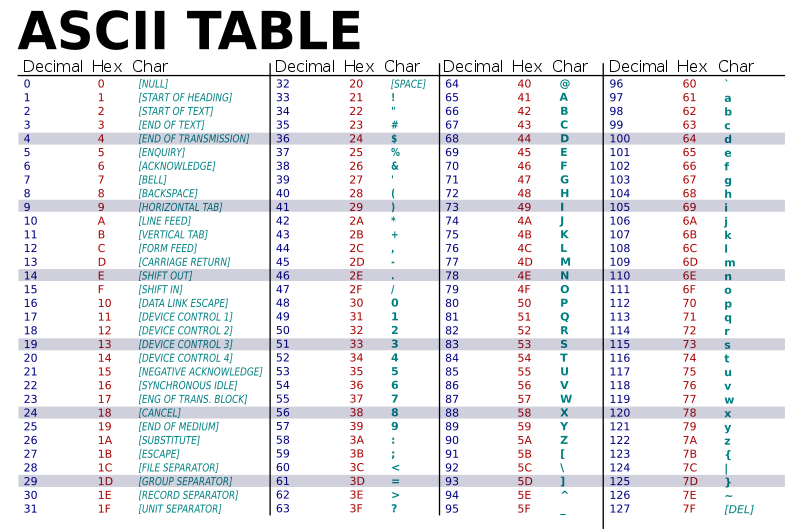
I programmering kallas en följd av bokstäver eller tecken för en sträng (string). I den här övningen arbetar vi enbart med versaler. Varje enskilt tecken kallas en char. Alla tecken i en dator representeras av tal enligt t.ex. ASCII-tabellen, där
A motsvarar talet 65,
B motsvarar 66, osv.
De svenska tecknen Å, Ä och Ö ligger inte i ordningsföljd med övriga bokstäver, därför skapar vi ett eget alfabet i stället för att använda ASCII rakt av. Moderna datorer använder ett ännu större antal tecken, de kallas för unicode.
Vår lösning kommer inte heller hantera mellanslag eller andra skiljetecken — vi fokuserar endast på själva bokstäverna.
Vårt alfabet¶
För att kunna räkna och hantera ÅÄÖ definierar vi vårt eget alfabet som en sträng (istället för att använda ASCII-koder). Vi begränsar oss till versaler:
alfabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZÅÄÖ"
Detta ger oss $N=29$ bokstäver.
Indexering och Modulo¶
Varje bokstav tilldelas ett index som börjar på 0:
A $\rightarrow$ Index 0
B $\rightarrow$ Index 1
Ö $\rightarrow$ Index 28
Att börja räkna på noll är avgörande för modulär aritmetik. Alla chifferberäkningar kommer att utföras modulo 29 ($\pmod{29}$).
Formel för kryptering¶
När vi krypterar vill vi att alfabetet ska “loopa runt” när vi passerar slutet. Till exempel: om vi skiftar Z tre steg åt höger vill vi hamna på C. Detta löser vi med modulo, som gör att talen automatiskt hoppar tillbaka till början av intervallet.
Om vårt alfabet innehåller 29 bokstäver (A–Ö) och vi vill skifta en bokstav n steg, kan krypteringsfunktionen skrivas som:
$$ E(x)=(x+n) \mod 29$$
där x är indexet för den bokstav vi vill kryptera.
modulo operatorn skrivs som % i python.
Exempel¶
$$ E(x)=(x+n) \mod 29$$
Låt oss kryptera bokstaven E med nyckeln $n=3$.
- Klartext: E är bokstav nummer 4 (A=0, B=1, C=2, D=3). Alltså $x=4$.
- Beräkning:$E(4) = (4 + 3) \pmod{29} = 7 \pmod{29}$
- Chiffer: $E=7$. Index 7 motsvarar bokstaven H.
Beräkna index och bokstav i python¶
För att ta reda på index av en bokstav använder vi oss koden nedan
alfabet.index('P')
15
För att se vilken bokstav som motsvarar index 4 kan vi skriva
alfabet[4]
'E'
I python uttrycks algoritmen på följande sätt:
char = 'Ö' #Bokstav att kryptera
n = alfabet.index(char) #Omvandla till ett tal mellan 0 och 29
encrypted = (n+3) % 29 #Skifta tre steg åt höger och räkna mod 29
newchar = alfabet[encrypted] #Omvandla till en bokstav
print(char,' blir krypterat', newchar)
Ö blir krypterat C
För att dechiffrera en bokstav gör vi helt enkelt det motsatta:
$$ D(x)=(x-n) \mod 29$$
Jag har här tänkt mig att vi skiftar "framåt" när vi krypterar och bakåt när vi dechiffrerar men det går naturligtvis att göra tvärtom.
# Dechiffrera bokstaven ovan
n = alfabet.index(newchar) #Omvandla till ett tal mellan 0 och 29
encrypted = (n-3) % 29 #Skifta tre steg åt vänster,
original_char=alfabet[encrypted] #Omvandla till klartext
print(newchar,' blir dekrypterat', original_char)
C blir dekrypterat Ö
Algoritm¶
Om vi vill kryptera en sträng behöver vi göra följande:
- Ta ut en bokstav ur strängen
- Omvandla den till ett tal (dess index i alfabetet)
- Säkerställa att talet är mellan 0 och 28 (29 bokstäver i vårt alfabetet)
- Skifta ett antal positioner med hjälp av modulo.
- Omvandla det nya värdet till en bokstav
Nedan ser du en funktion som krypterar en text med ett Ceasar-chiffer
# En funktion som skiftar bokstäver i en sträng n positioner
def ceasar_encrypt(my_text, shift):
result="" #Sträng för att bygga den krypterade texten
for i in range(len(my_text)):
bokstav = my_text[i] #Plocka ut en bokstav
n = alfabet.index(bokstav) #Omvandla till bokstavens index
encrypted = (n + shift) % 29 #Kryptera - skifta höger med modulo
result += alfabet[encrypted] #Lägg till bokstaven i result strängen
return result
Funktionen anropas enligt nedan:
scrambled=ceasar_encrypt("HELLO",4)
print(scrambled)
LIPPS
Vi kan vara lite listiga och använda samma funktion för att dekryptera, vi skickar bara in att vi vill skifta lika många steg bakåt.
secret2=ceasar_encrypt(scrambled,-4)
print(secret2)
HELLO
Det är väldigt enkelt att knäcka ett ceasarchiffer. Med en dator gör jag enkelt en "brute-force" attack där jag helt enkelt prövar att skifta det krypterade meddelandet med alla möjligheter.
for i in range (10): # Visa bara tio rader
print(-1*i,ceasar_encrypt(scrambled,-1*i))
0 LIPPS -1 KHOOR -2 JGNNQ -3 IFMMP -4 HELLO -5 GDKKN -6 FCJJM -7 EBIIL -8 DAHHK -9 CÖGGJ
Vigenèrechiffer¶
En vidareutveckling av ceasarchiffret där man använder ett nyckelord för att kryptera. Det var inte Vigenère som beskrev tekniken först utan han blev felaktigt förknippad med detta, metoden beskrevs av italienaren Giovan Battista Bellaso 1553. Det tog trehundra år innan man utvecklade systematiska metoder för att knäcka koder krypterade med den här metoden.

En avstickare...¶
Att en upptäckt namnges av någon annan än upptäckaren är så vanligt att Stephen Stigler, en professor i statistik, skrev Stigler's lag: "Inget fenomen är uppkallat efter den egentliga upptäckaren"
Stigler's lag upptäcktes enligt Stigler av Robert K. Merton.
Matematisk kan krypteringen beskrivas som
$$E_i = (P_i + K_i) \mod 29$$
där $P_i$ och $K_i$ är värdet för bokstaven på position $i$ vårt meddelande ($P$) och nykeln ($K$).
Dekryptering sker med formeln:
$$D_i = (E_i - K_i) \mod 29$$
Vårt alfabet innehåller 29 tecken.
Låt oss säga att vi vill kryptera "ATTACKATDAWN" och att vi använder en nyckel "MELON" för att kryptera.
Vi måste se till att vår nyckel är lika lång som texten, det gör vi enkelt genom att upprepa nyckeln.
ATTACKATDAWN
MELONMELONMEdef expand_key(plain_text, key):
if len(plain_text)== len(key):
return key
else:
long_key=""
for i in range(len(plain_text)):
long_key += (key[i % len(key)])
return long_key
Förläng nyckeln så att den blir lika lång som ditt meddelande¶
plain="ATTACKATDAWN"
key="MELON"
expanded_key = expand_key(plain, key)
print(expanded_key)
MELONMELONME
Funktion för att kryptera¶
$$E_i = (P_i + K_i) \mod 29$$
def vigenere_encrypt(my_text, key):
result=""
for i in range(len(my_text)): #Gå igenom bokstav för bokstav
n = alfabet.index(my_text[i]) #Hitta talet som motsvarar bokstaven
shift = alfabet.index( key[i]) #tal för hur mycket som ska skiftas
encrypted = (n + shift) % 29 #Räkna ut de krypterade talet
result += alfabet[encrypted] #Lägg till motsvarande bokstav i result
#Raden nedan skriver ut detaljer, kan utelämnas
print(f'{i:2}, {my_text[i]}, {key[i]}, {alfabet[encrypted]}')
return result
Kryptera "ATTACKATDAWN" med nyckel "MELON"¶
secret_msg=vigenere_encrypt(plain, expanded_key)
print('-' * 50)
print(plain ,'krypteras som ', secret_msg)
0, A, M, M 1, T, E, X 2, T, L, B 3, A, O, O 4, C, N, P 5, K, M, W 6, A, E, E 7, T, L, B 8, D, O, R 9, A, N, N 10, W, M, F 11, N, E, R -------------------------------------------------- ATTACKATDAWN krypteras som MXBOPWEBRNFR
Funktion för dechiffrering¶
$$D_i = (E_i - K_i) \mod 29$$
def vigenere_decrypt(my_text, key):
result=""
for i in range(len(my_text)):
encrypted = alfabet.index(my_text[i])
shift = alfabet.index( key[i] )
decrypted = (encrypted - shift) % 29
result += alfabet[decrypted]
#Raden nedan skriver ut detaljer, kan utelämnas
print(f'{i:2}, {my_text[i]}, {key[i]}, {alfabet[decrypted]}')
return result
Och så ska vi dechiffrera meddelandet¶
original_msg = vigenere_decrypt(secret_msg, expanded_key)
print('-' * 50)
print(original_msg)
0, M, M, A 1, X, E, T 2, B, L, T 3, O, O, A 4, P, N, C 5, W, M, K 6, E, E, A 7, B, L, T 8, R, O, D 9, N, N, A 10, F, M, W 11, R, E, N -------------------------------------------------- ATTACKATDAWN
Övning¶
Skapa ett kort meddelande och en nyckel med minst 10 tecken, kryptera ditt meddealnde och skicka detta till en klasskompis. Ge sedan nyckeln till din klasskompis.
Ditt meddelande och nyckel ska vara respektfullt.
Att på ett säkert sätt växla nycklar är en utmaning in kryptografi
Övning 2¶
I den här övningen behöver vi ett bättre alfabet så vi utökar alfabetet med gemener, siffror och specialtecknen.?=/ och vårt alfabet får följande utseende:
ABCDEFGHIJKLMNOPQRSTUVWXYZÅÄÖabcdefghijklmnopqrstuvwxyzåäö0123456789.?=:/
OBS Alfabetet ovan måste stå som en rad i din kod.
Vilka ändringar behöver du göra i din kod för att kunna kryptera och dekryptera med vårt uppdaterade alfabet? Ledtråd
len(alfabet)
73
Här är ett meddelande:
tEXTH3LÖÅÅL07/YXJUqYGSB450XG?14Åxm.cMrzZtbU
krypterat med nyckeln Matte5
Du ska dekryptera meddelandet.
Läsa mer¶
